Medical Insurance Cost - Exploratory Analysis

Photo by Towfiqu barbhuiya on Unsplash

Introduction & Objectives

Health insurance plays an important role in future financial planning. Insurance members are required to pay a routine payment (insurance rates) to the insurance company. This rate will be used to pay medical bill of the insurance members. therefore, determination of insurance rate becomes a critical component to ensure the sustainability of the insurance.

In this project, the author wanted to do an exploratory analysis based on known variable that may correlate with the medical bill of the said members. This project will be using personal medical bills dataset (insurance.zip) as the main source¹, along with the included metadata below:

1. age: age of primary beneficiary
2. sex: insurance contractor gender, female, male
3. bmi: body mass index, providing an understanding of body, weights that are relatively high or low relative to height, objective index of body weight (kg/m2) using the ratio of height to weight, ideally 18.5 to 24.9
4. children: number of children covered by health insurance / number of dependents
5. smoker: smoking
6. region: the beneficiary’s residential area in the US, northeast, southeast, southwest, northwest.
7. charges: individual medical costs billed by health insurance

At glance, bmi and smoker would likely to induce a high medical cost of a person, while age, sex, children and region may contribute in some senses or the others.

Objectives:

• Analyze the relationship between multiple variables to medical charges
• Characterize the risk profile of members, based on the said analysis
• Determine if the insurance rate can be optimized for each risk profile

Setting-up

#importing libraries
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import altair as alt 
# import hvplot.pandas

#setting default theme
sns.set_theme(style='white', palette='tab20') 

Importing Dataset

insurance = pd.read_csv('insurance.zip')
insurance.head()

	age	sex	bmi	children	smoker	region	charges
0	19	female	27.900	0	yes	southwest	16884.92400
1	18	male	33.770	1	no	southeast	1725.55230
2	28	male	33.000	3	no	southeast	4449.46200
3	33	male	22.705	0	no	northwest	21984.47061
4	32	male	28.880	0	no	northwest	3866.85520

Feature Engineering

In this dataset, the BMI is a numeric data. In order to better analyze the dataset, the bmi data can be grouped into different class/group. The classification in this project will be using BMI classification below:

BMI	Weight Status
Below 18.5	Underweight
18.5 – 24.9	Healthy Weight
25.0 – 29.9	Overweight
30.0 and Above	Obesity

We can use pandas.cut method to create a quick binning over bmi column.

bins= [0,18.49,24.9,30,100] #setting up the group based on bmi bins 
labels = [
         'underweight',
         'healthy',
         'overweight',
         'obese'
         ] #setting up the label on each group

insurance['bmi_class']= pd.cut(
   insurance['bmi'], 
   bins=bins, 
   labels=labels,
   include_lowest=False
   ) #making the new column called bmi_class

#sanity check on bmi_class
(insurance
 .groupby('bmi_class')
 [['bmi', 'bmi_class']]
 .agg(['min', 'max', 'count'])
 # .style.background_gradient()
 # .style.text_gradient()
#  .T
)

Table 1: BMI Class

	bmi			bmi_class
	min	max	count	min	max	count
bmi_class
underweight	15.96	18.335	20	underweight	underweight	20
healthy	18.50	24.890	222	healthy	healthy	222
overweight	24.97	30.000	391	overweight	overweight	391
obese	30.02	53.130	705	obese	obese	705

Table 1 shows a new column bmi_class as the result of grouping the bmi data into different categories.

Quicklook

insurance.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1338 entries, 0 to 1337
Data columns (total 8 columns):
 #   Column     Non-Null Count  Dtype   
---  ------     --------------  -----   
 0   age        1338 non-null   int64   
 1   sex        1338 non-null   object  
 2   bmi        1338 non-null   float64 
 3   children   1338 non-null   int64   
 4   smoker     1338 non-null   object  
 5   region     1338 non-null   object  
 6   charges    1338 non-null   float64 
 7   bmi_class  1338 non-null   category
dtypes: category(1), float64(2), int64(2), object(3)
memory usage: 74.8+ KB

The data appears to be clean, with no null row, and dftypes appear to be correct. However, the format appears to be a non-tidy format.

(insurance
 .select_dtypes(include=object) #includes all column with object dtypes
 .value_counts() #counting unique value
)

sex     smoker  region   
female  no      southwest    141
                southeast    139
                northwest    135
male    no      southeast    134
                northwest    132
female  no      northeast    132
male    no      southwest    126
                northeast    125
        yes     southeast     55
                northeast     38
                southwest     37
female  yes     southeast     36
                northeast     29
                northwest     29
male    yes     northwest     29
female  yes     southwest     21
Name: count, dtype: int64

Some observations:

• 2 categorical data in sex column: female and male
• 2 categorical data in the smoker column, yes or no
• 4 categorical data in the region column: southwest, northwest, southeast, and northeast

Important

The first attempt is to see the distribution on each variable relative to each other, depending on different categories. For example, comparing mean age between smoker and non-smoker group, age between low and high bmi class, etc.

Then trying to understand the relationship of each variable with respect to the medical charges

Exploratory Data Analysis

As many people know, smoking is highly linked to clinical disease such as TBC, lung cancer, hypertension, etc. People with smoking history, may be considered a high risk profile, and as the likely outcome the medical charges may be higher than a non-smoker people.

Overall Mean age of insurance member

(sns
 .displot(
     data=insurance, 
     x='age', 
     hue='smoker',
     kind='hist',
     height=3,
     aspect=1.2,
 )
);

Figure 1: Overall Mean Age

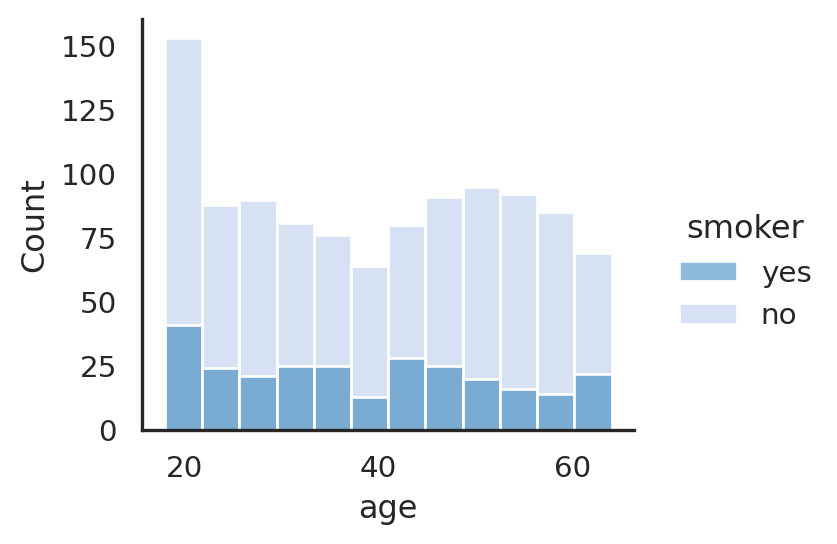
Based on distribution at Figure 1, the mean age for all insurance members is around 39 years old. There is also higher number of non-smoker compared to the total data (2 times higher) compared to smoker. There is an anomaly frequency around age of 20 that has up to 4 times higher counts. May need further check.

Mean age, bmi and charges of smoker at different sex

(insurance
 .groupby([
     'smoker',
     'sex'
 ])
 
 [[
     'age',
     'bmi',
     'charges'
  ]]
 
 .agg([
     'mean', 
 ])
#  .style.background_gradient(
#      axis=0,
#      cmap="Blues"
#  )
)

Table 2: Statistic of Age, BMI, and Charges by Smoker and Sex

		age	bmi	charges
		mean	mean	mean
smoker	sex
no	female	39.691042	30.539525	8762.297300
	male	39.061896	30.770580	8087.204731
yes	female	38.608696	29.608261	30678.996276
	male	38.446541	31.504182	33042.005975

Calculating the ratio of smoker to non-smoker group

(insurance
 .groupby('smoker')
 [['charges']]
 .agg([np.mean])/8434.268298 #to calculate how high the smoker medical charges
)

Table 3: Ratio of Charges based on Smoker profile

	charges
	mean
smoker
no	1.000000
yes	3.800001

Based on the above Table 2, the male bmi is always higher than the female counterpart, irrespective of its sex. Furthermore, the average bmi for smoker is slightly higher than non-smoker group.

On the other hand, the average age for female is always higher than its male counterpart, regardless of smoker or non-smoker.

As indicated by Table 3, the medical charges for is much higher in the smoker member, compared to non-smoker member, with up to 4 times higher for smoker

(insurance
 .groupby('sex')
 [['charges']]
 .agg([np.mean])/12569.578844 #to calculate how high the smoker medical charges
)

Table 4: Ratio of Charges based on Sex profile

	charges
	mean
sex
female	1.000000
male	1.110359

Furthermore, Table 4 shows that male has 10% higher medical charges compared to female counterpart.

Distribution of age categorized based on sex, smoker, and bmi_class

(sns
 .catplot
 (data=insurance,
  kind='box',
  x='age', 
  y='smoker',
  hue='bmi_class',
  col='sex',
  # col_wrap=1,
  height=4,
  aspect=0.7,
  # showmeans=True,
  palette='Blues',
 )
);

Figure 2: Age distribution based on Categorical values

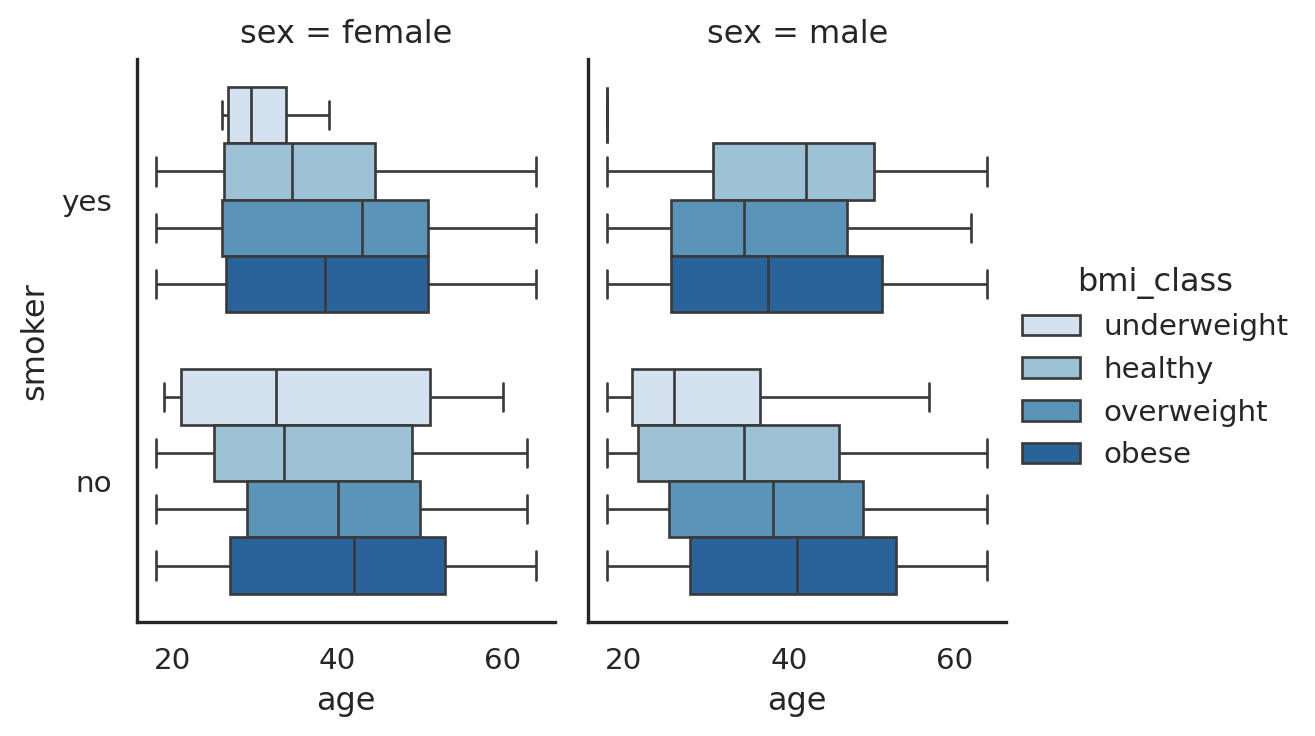
The above Figure 2 age shows a the distribution of age between smoker, bmi_class and different sex in the data. As can be seen, there is a clear trend of non-smoker where as the age increases, the bmi increases also, in both male and female group.

Whereas in the smoker group, there is no clear trend of age vs bmi. This can be further checked when using scatterplot between age and bmi vs charges.

Does region affecting the age distribution?

(sns
 .catplot
 (data=insurance,
  kind='box',
  x='age', 
  y='smoker',
  hue='bmi_class',
  col='region',
  col_wrap=2,
  height=4,
  aspect=0.7,
  showmeans=True,
  palette='Blues',
 )
);

Figure 3: Age distribution based on region

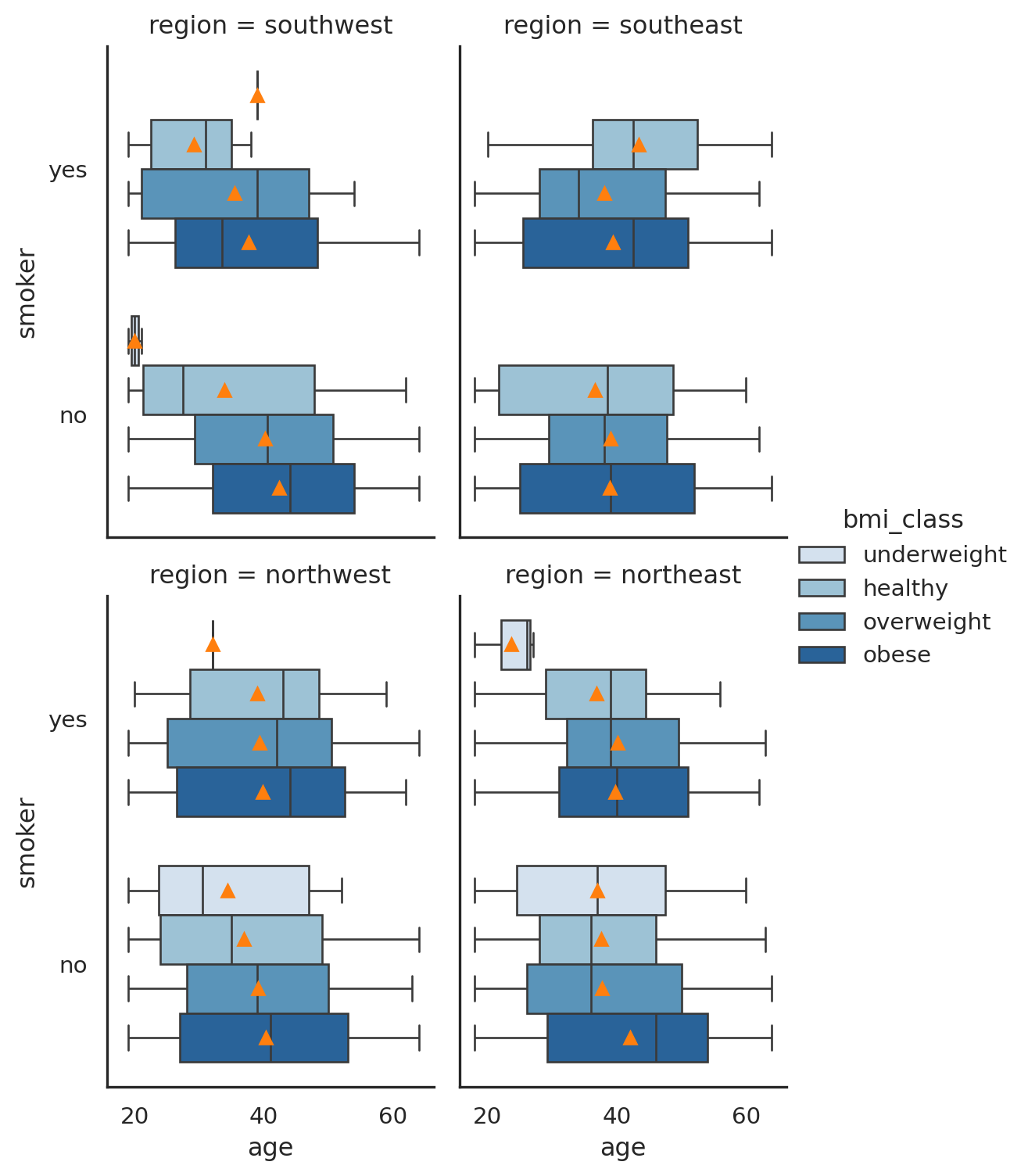
As can be seen in Figure 3, the region category does not seem to bring any value to the analysis, as the pattern with/ without region data is unclear. May need further check.

Inspecting the age vs charges based on smoker, sex, and bmi_class profile

g=(sns
.relplot
 (data=insurance,
  x='age',
  y='charges',
  hue='smoker',
  size='bmi_class',
  style='sex',
  # legend='full',
  # col='bmi_class',
  # col_wrap=1,
  height=3.5, 
  aspect=1.2,
  markers=["8","P"],
  palette='tab10',
  size_order=['obese', 'overweight', 'healthy', 'underweight']
 )
);

#setting up annotations

g.fig.text(0.6, 0.25, "I",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

g.fig.text(0.6, 0.45, "II",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

g.fig.text(0.6, 0.7, "III",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

plt.suptitle('age vs charges', y = 1.05);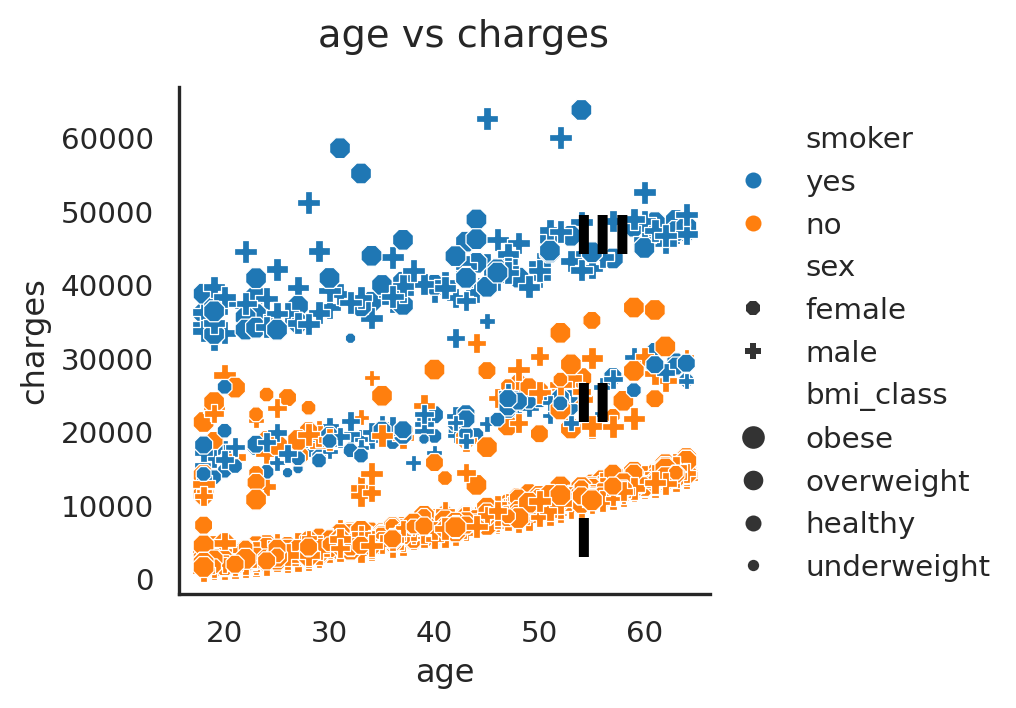

Figure 4: Age vs Charges

Figure 4 shows at least three groups of trend with a strong relationship between medical charges and age. As the age increases, the medical charges increases.

The three group of medical charges are as follows:

• group I: 16000 and below
• group II: 16000-30000
• group III: above 30000

The three group of trends were heavily affected by the smoker/ non-smoker group, as the highest group III appears to have more points with obese bmi_class. This can be further checked if we exclude non-smoker group and hue it by bmi_class, and we can put sex as the column category.

Does sex affects age vs charges distribution/trend?

(sns
.relplot
 (data=insurance
  # .query("smoker=='yes'")
  ,
  x='age',
  y='charges',
  hue='bmi_class',
  size='bmi_class',
  style='smoker',
  # legend='full',
  col='sex',
#   col_wrap=1,
  # row='smoker',
  height=4, 
  aspect=0.7,
  markers=["8","P"],
  s=300,
  palette='tab10',
  alpha=0.7,
  size_order=['obese', 'overweight', 'healthy', 'underweight'],
  
 )
)

plt.suptitle('age vs charges | separated by male vs female', y = 1.05);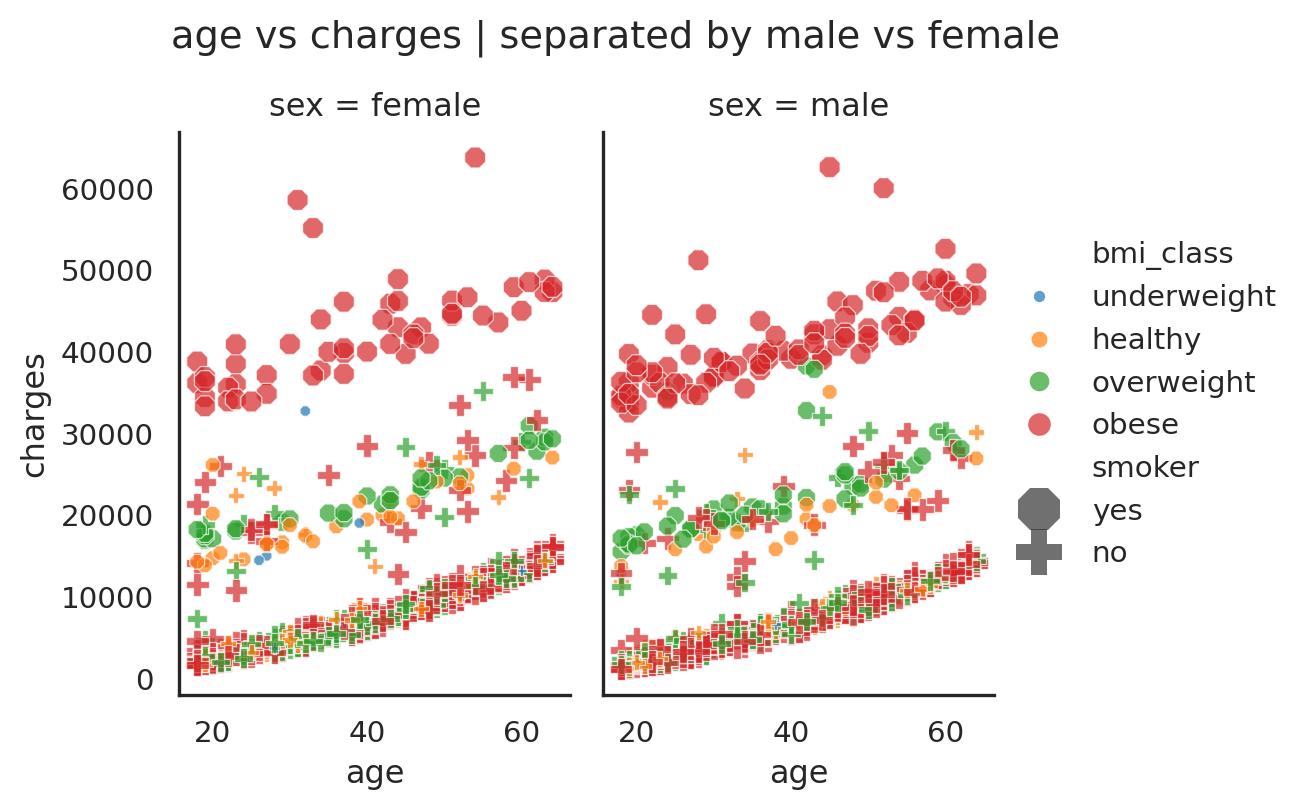

Figure 5: Age vs Charges based on Sex

Couple conclusions can be drawn from these Figure 4 and Figure 5:

1. That the male is likely to have higher medical charges compared to female, with relatively small difference (Table 4).
2. There are three groups of strong trend between age vs charges, where as the age increases in all trends, the medical charges is likely to increases as well.
3. The three groups can be characterized from low-high charges as follows:
   1. Group I: medical charges between 0-16,000, predominantly non-smoker,and a mix between all bmi_class.
   2. Group II: medical charges between 12,000-30,000, a mix between smoker and non-smoker group, and bmi_class of healthy and overweight.
   3. Group III: medical charges above 30,000, predominantly obese bmi_class and smoker.

Some observed outlier (group I-a) between group I and II?

g = (sns
.relplot
 (data=insurance,
  x='age',
  y='charges',
  hue='bmi_class',
  size='bmi_class',
  style='smoker',
  # legend='full',
  col='smoker',
  # col_wrap=1,
  # row='smoker',
  height=4, 
  aspect=0.7,
  markers=["8","P"],
  s=300,
  palette='tab10',
  alpha=0.7,
  size_order=['obese', 'overweight', 'healthy', 'underweight'],
 )
);

#annotations

g.fig.text(0.6, 0.22, "I",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

g.fig.text(0.3, 0.4, "II",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

g.fig.text(0.3, 0.63, "III",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )

g.fig.text(0.65, 0.4, "I-a",
   color="black", fontdict=dict(size=20), fontweight='bold'
          )


plt.suptitle('age vs charges | separated by smoker vs non-smoker', y = 1.05);

Figure 6: Outliers?

If we look at the above Figure 6, in the non-smoker group, there is a cloud of data below the group II is. This needs further check, as what would affect the scattered data across this category, as it looks like there is another factor (aside from what was plotted already) that affects the data “moves up” (increased medical charges)

What affects the outlier/ I-a group?

(sns
.relplot
 (data=insurance.query('smoker == "no"'),
  x='age',
  y='charges',
  hue='bmi_class',
  # size='children',
  style='sex',
  legend='full',
  col='children',
  col_wrap=2,
  # row='region',
  height=3, 
  aspect=1,
#   markers=["8","P"],
  # s=400,
  palette='tab10',
  alpha=0.7,
  # size_order=['obese', 'overweight', 'healthy', 'underweight'],
 )
);

Figure 7: Outliers vs number of Children

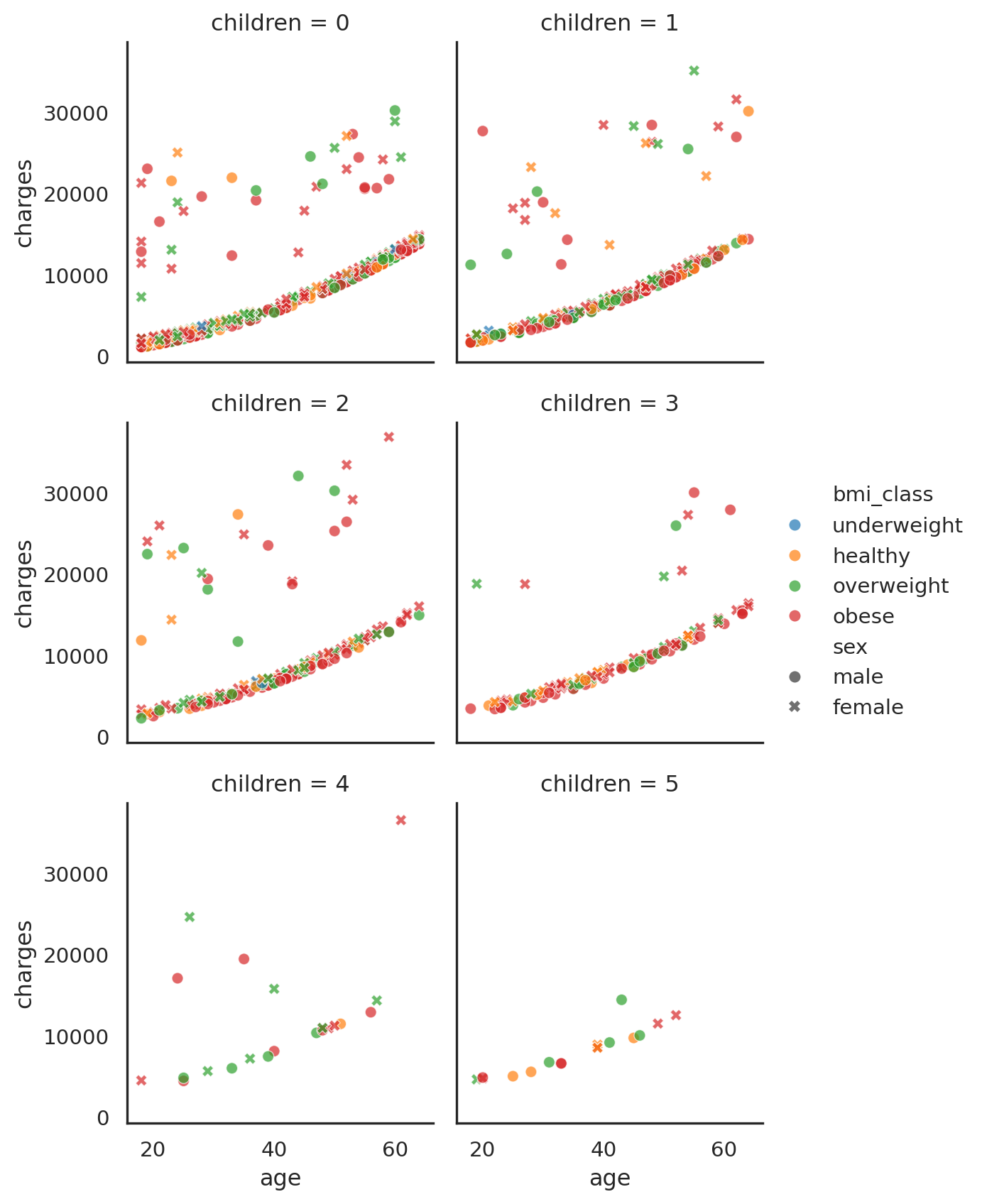
Figure 7 shows just group I and I-a where we see through zero to six number of childrens, colored by bmi_class and styled by sex. As can be seen, there is no clear differentiator between group I and I-a, as the number of children increases, it affects both group I and I-a also.

Important

It is unclear as to why this is happening. Perhaps other factors plays a role. At the time of this writing, author decided to categorized the group I-a as the outlier.

g = (sns
.relplot
 (data=insurance,
  x='bmi',
  y='charges',
  hue='smoker',
  size='children',
  # style='sex',
  # legend='full',
  # col='bmi_class',
  # col_wrap=1,
  height=3.5, 
  aspect=1,
  markers=["8","P"],
  palette='tab10',
  size_order=[1,2,3,4,5,6]
 )
)

#annotations
g.fig.text(0.35, 0.25, "I",
   color="black", fontdict=dict(size=18), fontweight='bold'
          )

g.fig.text(0.35, 0.45, "II",
   color="black", fontdict=dict(size=18), fontweight='bold'
          )

g.fig.text(0.6, 0.65, "III",
   color="black", fontdict=dict(size=18), fontweight='bold'
          )

g.fig.text(0.5, 0.45, "I-a",
   color="black", fontdict=dict(size=18), fontweight='bold'
          )

plt.suptitle('bmi vs charges', y = 1.05);

Figure 8: BMI vs Charges

Similar to the previous Figure 5, in Figure 8 we can see that the non-smoker group overlaps with the smoker group at around 16,000-30,000 medical charge range.

Conclusions and Outcomes

1. The insurance member can be characterzed based on the smoker profile, age, bmi/ bmi_class, and sex profile.

2. The critical factor for a high medical charges is whether member is a smoker or not, followed by age and then bmi².

3. Other variable such as the number of children/ dependant is not playing a role, whereas sex profile affect the charges slightly³.

4. There is a strong relationship between age and medical charges, with 3 strong group categorized by smoker and bmi profile. The big three groups are:

   • Group I: medical charges below 16k, related to a group of non-smoker⁴.
   • Group II: medical charges between 16k-30k, related to a group of smoker and overweight.
   • Group III: medical charges above 30k, related to a group of smoker and obese.

   These three groups have its own trendline which can be later determined (trendline).

5. There is also one outlier or group I-a, where it is unclear as to what affects the medical charges increase to be between group I and II.

The above groups (I, II, III) can be used for risk profiling, where based on its profile, the associated risk related to medical charges can be determined. Since each group forms a trendline (simple linear regression), and can be categorized based on its smoker, and bmi profile. Based on this approach, one can estimate the optimum pricing for each risk profile (based on its medical charges).

See below flowchart for simple ilustration.

flowchart LR
    A[Member] --> B{Smoking}
    B --> |No| C[trendline Group I]
    B --> |Yes| D{BMI Class}
    D --> |Overweight| E[trendline Group II]
    D --> |Obese| F[trendline Group III]

Note

The next step would be using some of these knowledge to further investigate the likelihood (probability) of each risk profile based on its numeric (age-bmi) and categorical variable (smoker-bmi-region-sex).

---

Important

This article was made as a replacement for medium article as part of Pacmann Data Science bootcamp assignment for Linear Algebra batch 8. The EDA notebook can be found in this notebook. Inside there will be a Youtube link as part of the assignment also.

Footnotes

1. also available at Kaggle.

2. the lowest medical charges (group I) may have obese in their profile, but since it is a non-smoker profile, the medical charges is lower.

3. around 10% higher in male, compared to female counterpart (see Table 4)

4. the BMI class shows a mix of all classes (from underweight to obese)